همنهشتی و تئوری اعداد



اگر m یک عدد طبیعی و a وb دو عدد صحیح باشند، و m بتواند اختلاف بین a و b را بشمارد، آنگاه می‌گوییم a همنهشت است با b به پیمانه m.

تعریف

اگر a و b اعدادی صحیح و m عددی طبیعی باشد گوییم a همنهشت است با b به پیمانه m هرگاه (m|(b-a و می‌نویسیم (به پیمانه m)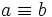 یا .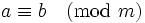

  • رابطه همنهشتی یک رایطه هم‌ارزی است پس این رابطه می‌تواند مجموعه اعداد صحیح را افراز کند. به مثال 2 در این زمینه توجه کنید.

ویژگی‌های همنهشتی

  • اگر b≡a به پیمانه m آنگاه به ازای عدد صحیح c داریم: a+c ≡ b+c به پیمانه m .
  • اگر b و a باهم همنهشت و (d=(a,b و c≡d به پیمانه m آنگاه ac≡bc به پیمانه m.
  • اگر b≡a به پیمانه m ، آنگاه به ازای n های طبیعی 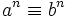به پیمانه m.
  • به ازای تمام aوb های همنهشت به پیمانه m مجموع و حاصلضرب متناظرشان نیز باهم همنهشتند به پیمانه m.
  • اگر b≡a به پیمانه m و c عدد صحیحی باشد، آنگاه ac≡bc به پیمانه m.

قضایای مربوط به همنهشتی

  1. اگر ac≡bc به پیمانه m و m,c)=d) آنگاهa≡b به پیمانه m/d.

لم مربوط به همنهشتی:

  1. اگر a≡b به پیمانه m باشد و d یکی ازمقسوم علیه های m باشد آنگاه a≡b به پیمانه d.
  2. اگر ac≡bc به پیمانه m و m,c)=1) آنگاه a≡b به پیمانه m.
  3. اگر r باقیمانده تقسیم a بر m باشد، انگاه، a≡r به پیمانه m.

مثال

  1. .
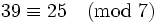  2. مجموعه اعدادی را بیابید که اختلافشان بر عدد 2 بخش پذیر باشد.
جواب:
طبق الگوریتم تقسیم داریم a=2q+r , 0≤r<2 ؛ یعنی a=2q یا a=2q+1.

پس کلاس هم‌ارزی 0 یا اعداد بخش‌پذیر بر 2 عبارت است از

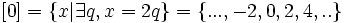
به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است.

و همچنین کلاس هم‌ارزی 1عبارت است از

به طوری که اختلاف این اعداد با عدد 2 نیز همواره بر 2 بخش پذیر است.

همچنین ببینید:

تعداد بازدید ها: 64303