مساله‌ی توزیع اعداد اول در اعداد صحیح همیشه در بین ریاضی‌دانان مورد بحث و پژوهش قرار داشته و دارد. از جمله‌ی مسائل در این موضوع پیدا کردن فرمول حسابی برای یافتن اعداد می‌باشد. یعنی فرمول‌هایی که فقط عدد اول تولید کنند، هر چند همه آنها به دست ندهند. از جمله فرمول‌های قدیمی و معروف در این زمینه منسوب به مرسن است. به اعداد به شکل 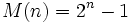اعداد مرسن گویند. مثال‌های ساده‌ای نشانگر اینند که این فرمول ممکن است عدد اول تولید نکند. مثلا 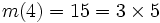. جدول زیر لیست اعداد اول کشف شده می‌باشد:

#	n	(M(n	تعداد رقم‌های (M(n	تاریخ کشف	کاشف
1	2		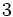1	مشخص نیست	ناشناس
2	3		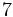1	مشخص نیست	ناشناس
3	5		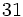2	مشخص نیست	ناشناس
4	7		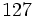3	مشخص نیست	ناشناس
5	13		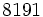4	1456	ناشناس
6	17		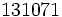6	1588	Cataldi
7	19		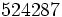6	1588	Cataldi
8	31		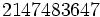10	1772	Euler
9	61		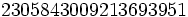19	1883	Pervushin
10	89		27	1911	Powers
11	107		33	1914	Powers
12	127		39	1876	Lucas
13	521		157	January 30, 1952	Robinson
14	607		183	January 30, 1952	Robinson
15	1,279		386	June 25, 1952	Robinson
16	2,203		664	October 7, 1952	Robinson
17	2,281		687	October 9, 1952	Robinson
18	3,217		969	September 8, 1957	Riesel
19	4,253		1,281	November 3, 1961	Hurwitz
20	4,423		1,332	November 3, 1961	Hurwitz
21	9,689		2,917	May 11, 1963	Gillies
22	9,941		2,993	May 16, 1963	Gillies
23	11,213		3,376	June 2, 1963	Gillies
24	19,937		6,002	March 4, 1971	Tuckerman
25	21,701		6,533	October 30, 1978	Noll & Nickel
26	23,209		6,987	February 9, 1979	Noll
27	44,497		13,395	April 8, 1979	Nelson & Slowinski
28	86,243		25,962	September 25, 1982	Slowinski
29	110,503		33,265	January 28, 1988	Colquitt & Welsh
30	132,049		39,751	September 20, 1983	Slowinski
31	216,091		65,050	September 6, 1985	Slowinski
32	756,839		227,832	February 19, 1992	Slowinski & Gage
33	859,433		258,716	January 10, 1994	Slowinski & Gage
34	1,257,787		378,632	September 3, 1996	Slowinski & Gage
35	1,398,269		420,921	November 13, 1996	GIMPS / Joel Armengaud
36	2,976,221		895,932	August 24, 1997	GIMPS / Gordon Spence
37	3,021,377		909,526	January 27, 1998	GIMPS / Roland Clarkson
38	6,972,593		2,098,960	June 1, 1999	GIMPS / Nayan Hajratwala
39	13,466,917		4,053,946	November 14, 2001	GIMPS / Michael Cameron
40	20,996,011		6,320,430	November 17, 2003	GIMPS / Michael Shafer
41	24,036,583		7,235,733	May 15, 2004	GIMPS / Josh Findley
42	25,964,951		7,816,230	February 18, 2005	GIMPS / Martin Nowak

فرما این حدس مشهور را (که حکمی قطعی نبود) مطرح کرد که همه عددهای به شکل



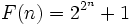
اول‌اند. در واقع به ازای n=1,2,3,4 داریم







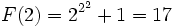
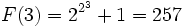
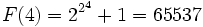
که همه اول‌اند. اما اویلر در سال 1732 تجزیه 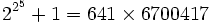را کشف کرد. پس (F(5 اعداد اول نیست. بعداً اول نبودن تعداد دیگری از این «عددهای فرما» هم معلوم شد؛ به دلیل دشواری اجتناب‌ناپذیر محاسبه مستقیم، روشهای عمیقتری برای تحقیق در هر مورد لازم است. تا کنون، اول بودن (F(n به ازای هیچ مقدار n>4 ثابت نشده است.
فرمول ساده و جالب توجه دیگری که عددهای اول بسیاری تولید می‌کند، فرمول



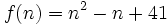
است به ازای(n=1,2,3,…,40، f(n اول است؛ به ازای n=41، داریم 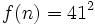که اول نیست. عبارت



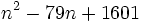
به ازای همه nها تا n=79 اعداد اول را به دست می‌دهد اما به ازای n=80، عدد حاصل اول .

---

همچنین ببینید

• اعداد اول
• اعداد مرسن
• فرما

---

پیوندهای خارجی

http://mathworld.wolfram.com/PrimeFormulas.html