ورود به مطلب
برای اینکه بتوان مسالههای تازه ریاضی را حل کرد، قبل از هر چیز ، باید با روشهای حل مساله آشنا بود. این روشها ، چندان زیادند که برای تجزیه و تحلیل همه آنها باید صفحههای زیادی را سیاه کرد.
کاشانی گفته است: اگر کسی تنها برخی قضیهها و دستورهای ریاضی را بداند و نتواند مسالههای تازهای که در
ریاضیات و یا حالتهای کاربردی آن در برابر او قرار میگیرد، حل کند، ریاضیدان نیست. ریاضیدان کسی است که از عهده حل مسالههای تازه برآید.
شباهت مساله با مسالههایی سادهتر
مسالهای در برابر شماست که راهحل آن را نمیدانید. در برابر خود ، این پرسشها را قرار دهید و تلاش کنید، پاسخ آنها را پیدا کنید: آیا این مساله ، حالت یا حالتهای خاصی دارد؟ آیا مسالهای سادهتر ، که با این مساله ، شباهت داشته باشد، به یادتان میآید؟ آیا میتوانید با رسم شکلهای مختلف یا با آزمایش عددهای مختلف ، مساله را عینیتر و ملموستر کنید؟ ... پرسشهایی از این گونه ، میتواند شما را با مساله آشناتر کند، به جز آن ، مسالههای دیگری در برابر شما قرار گیرد که از مساله اصلی سادهتر و احتمال حل آنها بیشتر است. و بعد ، اگر این مساله یا مسالههای سادهتر را حل کردید، از خود بپرسید: آیا میتوان از همین راهحل ، و راهحلی شبیه آن ، مساله اصلی را حل کرد؟ در راهحل مساله سادهتر ، چه تغییری بدهیم تا بتواند برای حل مساله ما مفید باشد؟ و ... .
البته در پیداکردن مسالههای مشابه و یا به اصطلاح "
شبیه سازی" باید مواظب دام و گمراهی بود و هر شباهتی ما را به نتیجه نمیرساند؛ تنها شبیه بودن، نمیتواند پایه"ای برای نتیجهگیری باشد. باید به یک نکته اساسی توجه کنیم که در مسالههای ریاضی ، "شباهت" میتواند وسیله و راهنمای ما برای کشف مسالههای تازه و یا احتمال وجود یک ویژگی در یک شکل یا یک دستور باشد، ولی نمیتواند جانشین استدلال شود، در ریاضیات ، برای پذیرفتن یک ویژگی با یک قاعده ، باید وجود و درستی آن ، با
استدلال منطقی ثابت شود.
روش برهان خلف
"برهان خلف" یکی از روشهای جالب ، برای اثبات قضیهها در
جبر و
هندسه است. در
برهان خلف ، به جای اینکه درستی یک گزاره را بطور مستقیم ثابت کنیم، راهی غیر مستقیم انتخاب میکنیم و ثابت میکنیم با نپذیرفتن درستی گزاره ، به نتیجهای نامعقول میرسیم. اصطلاح برهان خلف ، ترجمهای از واژه لاتین Reduction ad absurdum ، به معنای "اثبات از جهت مخالف" یا "اثبات از راه ردکردن حکم مخالف" است. تا آنجا که میدانیم،
اقلیدس نخستین کسی بود که از "برهان خلف" در کتاب مشهور خود به نام "مقدمات" استفاده کرد. او آن را "معمای برهان خلف" مینامید. و درباره آن ، میگفت: "گزاره A را میتوان ثابت شده دانست، وقتی که ، اگر آن را نادرست بدانیم، باز هم درستی A را نتیجه بدهد." و یا "اگر
گزاره A را بپذیریم و به تناقض برخورد کنیم، به این معناستن که باید A را بپذیریم."
روش ضریبهای نامعین
روش استفاده از
ضریبهای نامعین ، روش ساده ، در ضمن نیرومند ، برای حل برخی از مسالههای مربوط به جبر محاسبهای است. این روش را به تقریب ، میتوان این طور تعریف کرد:
وقتی منظور از حل مساله ، پیدا کردن یک چند جملهای باشد، مساله را حل شده فرض میکنیم و چندجملهای مورد نظر را (که با توجه به شروط مساله ، از درجه آن آگاهیم)، با ضریبهای مجهول (نامعین) مینویسیم. سپس با انجام عملهای ناشی از شروط مساله ، خود را به دستگاهی از معادلهها میرسانیم که مجهول آنها ، همان ضریبهای نامعین باشند و سرانجام ، با حل دستگاه (اگر شدنی باشد)، مقدار ضریبها و در نتیجه چند جملهای مورد نظر را پیدا میکنیم. روش ضریبهای نامعین تا حد زیادی ، ما را قانع میکند که مساله قابل حل است. ولی اگر با دستگاههای بزرگ سروکار پیدا کردیم، یا با دستگاهی روبرو شدیم که شامل معادلههای غیر خطی است. امکان حل آن در اختیار ما نیست و یا سرانجام ، اگر با محاسبههای طولانی و ملالآور روبرو شویم، باید در جستجوی راهحل دیگری برای مساله باشیم.
روش استقرای ریاضی
روش استقرای ریاضی را برای نخستین بار ،
بلز پاسکال (1623-1662) فیزیکدان ، فیلسوف و ریاضیدان فرانسوی در یکی از دنبالههای خود به کار برد و از آن مورد استفاده بسیاری از ریاضیدانان قرار گرفت. روش استقرای ریاضی در مسالههایی کاربرد دارد که به نحوی با
دنباله عددهای طبیعی سروکار داشته باشد. روش استقرای ریاضی از سه مرحله میگذرد:
- حدس جواب: در برخی حالتها جواب را به ما میدهند.
- آزمایش جواب: برای کوچکترین عدد طبیعی. در برخی حالتها ، این کوچکترین مقدار برابر صفر است.
- عبور از k به k+1: یعنی فرض کنیم جواب برای هر عدد طبیعی k درست است و ثابت کنیم، در اینصورت برای عدد طبیعی k+1 هم درست است.
روش استقرای ریاضی را روش استقرای کامل هم میگویند و یکی از نیرومندترین روشها برای اثبات دستورها و قضیههایی که برای همه عددهای طبیعی درستاند، بکار میرود.
استفاده از عبارتهای متقارن
عبارتهای دوری
عبارت جبری شامل n حرف l,m,...,c,b,a را دوری گویند، وقتی که با تبدیل a به b ، b به c ،...، l به m و m به a تغییر نکند. عبارت xy نسبت به x و y یک عبارت دوری است، زیرا با تبدیل x به y و y به x تغییر نمیکند. همچنین عبارت (z-x)(y-z)(x-y) نسبت به سه حرف x ، y و z دوری است: با تبدیل x به y ، y به z و z به x تغییر نمیکند.
عبارتهای متقارن
عبارتی را که شامل n حرف است، نسبت به این n حرف متقارن گویند، وقتی که با تبدیل هر دو حرف دلخواه آن به یکدیگر ، تغییر نکند. عبارت
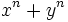
نسبت به x و y متقارن است، زیرا با تبدیل x به y و y به x تغییر نمیکند. ولی عبارت
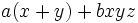
، نسبت به x و y متقارن است، ولی نسبت به x و y و z متقارن نیست.
سادهترین رابطههای متقارن بین ریشهها و ضریبهای یک چندجملهای
میدانیم معادله به صورت
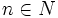
و
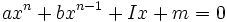
، اگر همه ریشهها را (حقیقی و موهومی) به حساب آوریم، دارای n ریشه است، بین ریشهها و ضریبهای معادله میتوان رابطههایی بدست آورد.
استفاده از تقارن در معادلههای مثلثاتی
فرض میکنیم:
یعنی f نسبت به sinx و cosx متقارن باشد. در اینصورت میتوان معادله f=0 را بر حسب
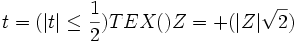
نوشت و در ضمن z و t با برابری
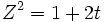
به هم مربوطند.
مباحث مرتبط با عنوان