حد
در بخش قبلی تابع معرفی شد. حال نوبت به مفهومی به نام حد (Limit) در ریاضیات میرسد.
حتماً تا بحال نام «بینهایت» (Infinity) را در ریاضیات شنیدهاید. اساساً مفهوم بینهایت یک مفهوم جدی است. یعنی اینکه بینهایت را آن چیزی در نظر میگیریم که از تمام اعداد بزرگتر باشد.
یا
به هر صورت بینهایت آن چیزی است که هیچگاه به آن نمیتوان رسید و حد بالای تمام اعداد است.
فرض کنید طول پارهخطی به مقدار واحد را نصف کنیم. سپس آن نصف را مجدداً نصف کنیم و … در نهایت چه عددی حاصل خواهد شد؟
بعد از
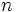
مرتبه نصفکردن مقدار طول حاصل
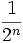
خواهد بود.
اگر بتوانیم بینهایت بار نصف کنیم مقدار طول چقدر میشود؟ اعداد بدست آمده نشان میدهند که
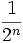
یواش یواش با افزایش
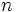
به سمت صفر میرود. ولی آیا مقدار
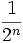
هیچگاه صفر خواهد شد؟ قطعاً نه بلکه اگر به سمت
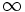
برویم مقدار
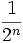
به سمت صفر میرود. به بیان ریاضی خواهد شد.
در تمام تعابیر بالا اگر
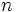
میل کند به بینهایت،
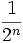
میل میکند به سمت صفر یعنی حد
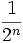
وقتی
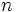
به سمت بینهایت میرود صفر است.
من قصد بیان دقیقتر حد را ندارم ولی در کتب مختلف " حساب دیفرانسیل و انتگرال" میتوان تعریف دقیق ریاضی آن را ببینید.
بیایید تابع حقیقی
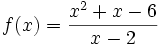
را بررسی کنیم.
مطابق با ضابطه تابع در
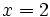
خواهیم داشت
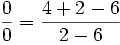
که بیمعنا است. ولی در بقیه مقادیر
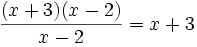
، نمودار تابع را نیز میبینید که شامل تمام نقاط
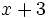
هست به غیر از
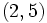
.
حال سؤال اینجاست که اگر ما مثلاً از سمت راست بینهایت بار به نقطه
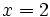
نزدیک شویم انتظار داریم مقدار تابع به کدام عدد نزدیک شود؟
طبیعی است که به عدد 5 گرچه هیچگاه مقدار نخواهد شد ولی حد تابع وقتی
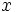
به 2 نزدیک میشود برابر 5 است.
در مورد نقطه دیگر مثلاً
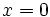
چطور؟ در اینجا
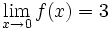
خواهد شد که مقدار خود تابع نیز
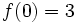
میباشد.
حال فرض کنید تابع به فرم
در این حالت حدس میزنید
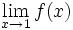
چقدر باشد؟
1 ، 4 یا هیچکدام؟
در این حالت حد تابع همان 1 است. درست است که مقدار تابع یعنی
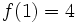
است ولی انتظارات ما وقتی خیلی (بینهایت بار) به
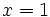
نزدیک میشویم از خروجی تابع عدد 1 است نه 4.
مثال
حال تابع
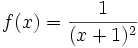
را در نظر بگیرید.
مقدار
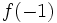
و
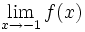
را بدست آورید. مقدار
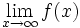
چقدر است.
جواب.
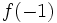
که وجود ندارد زیرا
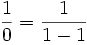
معنایی ندارد.
امّا در مورد حد آن چطور، بیایید به نمودار تابع نگاهی بیندازیم.
میبینید هر چقدر از هر دو طرف به
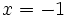
نزدیک میشویم تابع بدون هیچ محدودیتی همواره زیاد میشود و این همان تعریف بینهایت است.
پس
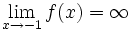
در مورد حد آخر بدیهی است هر چقدر
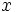
زیاد شود
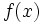
به صفر نزدیک میشود.
پس
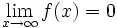
•پیوستگی به معنای دقیق یعنی آن که حد تابع در نقطه پیوسته با مقدارش یکی شود.
این را میتوانید مثلاً در مورد تمام مثالهای قبلی امتحان کنید و برابری این تعریف را با شهودمان از تابع پیوسته مطابقت دهید.
مثال
{* حد 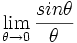 را حساب کنید.
را حساب کنید.
جواب.
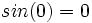 پس حد در حالت
پس حد در حالت 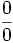 اتفاق میافتد که قطعاً تابع مقداری ندارد.
اتفاق میافتد که قطعاً تابع مقداری ندارد.
برای حل این حد از یک نامساوی مثلثاتی استفاده میکنیم:
بر روی دایره مثلثاتی این نامساوی بدیهی خواهد بود. (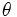 همیشه برحسب رادیان است.) فرض کنید
همیشه برحسب رادیان است.) فرض کنید  باشد آنگاه:
باشد آنگاه:
میدانیم که پس مقدار
پس مقدار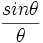 در حد به سمت صفر در نامساوی زیر قرار خواهد گرفت:
در حد به سمت صفر در نامساوی زیر قرار خواهد گرفت:
که بدیهی است میبایست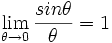 باشد.
باشد.
در حل این مثال به طور ضمنی از قضیه ساندویچ (Squeeze Theorem) استفاده شد که میگوید:
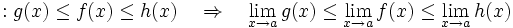
(حواشی
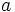
)
مثال
{* حاصل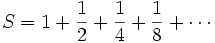 چه میشود؟
چه میشود؟
جواب. در اینجا ما با یک فرآیند جمعکردن بینهایتی روبرو هستیم که قطعاً و عملاً ممکن نیست ولی میتوان آنرا ابتدا درست تعریف کرد و پس از آن با مفهوم حد آن را جمع بست.
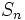 را به صورت زیر تعریف میکنیم:
را به صورت زیر تعریف میکنیم:
طبق تصاعد هندسی میدانیم مقدار آن خواهد شد:
حال جمع بینهایت جمله به معنای آن است که حد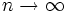 را حساب کنیم:
را حساب کنیم:
قضایایی در حد هستند که میتوانند برای حل مسائل مفید باشند گرچه خیلی از آنها بدیهیهستند ولی گفتنشان خالی از فایده نیست:
اگر
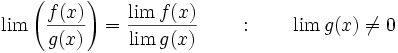
اگر 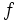 در
در 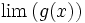 پیوسته باشد:
پیوسته باشد: 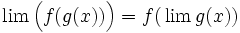
پیوند های خارجی
http://Olympiad.roshd.ir/physics/content/pdf/0034.pdf