مختصات دکارتی
مثل همیشه ابتدا سراغ مختصات دكارتی میرویم.
همانطور كه قبلاً هم گفته بودیم خوبی مختصات دكارتی به ثابت بودن بردارهای یكه آن یعنی
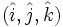
است و در مسائلی كه با جهتگیریهای ثابت مواجه هستیم مفید میشود.
مثال
ذرهای تحت شتابی است كه از رابطه
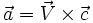
بدست میآید كه
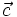
بردار ثابتی است. (این شتاب ذرات باردار در یك میدان مغناطیسی یكنواخت است) حركت كلی كه این نوع شتاب ایجاد میكند چگونه است؟
حل.
برای سادگی جهتگیری مختصاتمان را بگونهای میگیریم كه
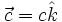
شود:
بطور بدیهی
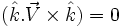
است و مؤلفهای در راستای
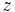
ندارد پس
ثابت:
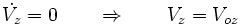
میماند دو مختصه دیگر
جواب این معادله به فرم
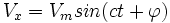
است.
برای بدست آوردن مكان برحسب زمان كافی است از سرعتها نسبت به زمان مشتق بگیریم:
منتها قبل از آن بهتر است در مورد
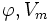
و نحوه بدست آمدن آنها صحبت كنیم.
این دو پارامتر ضرایبی هستند كه از شرایط اولیه سرعتها بدست میآیند:
میتوان دید كه
از اینجا پیداست كه
حال برویم سراغ بدست آوردن
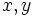
امّا این چه شكل هندسی دارد.
چنانچه در یك
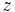
ثابت به
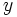
و

نگاه كنیم و برای سادگی تصور
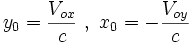
آنگاه
كه
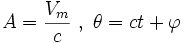
. این معادلات نقاط دایرهای را در مختصات دكارتی معین میكنند. پس تصویر
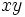
حركت ذره دایره است. اگر این دایره را به ازای
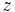
های مختلف كش بدهیم شكلی فنری (مارپیچی) یا Helix ایجاد خواهد شد.
مارپیچی كه در امتداد
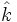
(همان
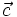
) كش آمده است.
مسائل دیگر را نیز میتوان در مختصات دكارتی (سه بعدی) بررسی كرد، منتها معمولاً جزء مسائل عمومی نیستند. اكثر مسائل عمومی بعلت تقارنهای خاص جهان در مختصات كروی بررسی میشوند كه موضوع مورد بحث بخشهای آینده است.
پیوند های خارجی
http://Olympiad.roshd.ir/physics/content/pdf/0066.pdf