اگر

به عنوان n شی دو به دو متمایز باشند آنگاه هر حال کنار هم قرار گرفتن این n شی کنار هم در یک ردیف را یک جایگشت از این n شی می گوییم. برای ردیف کردن این n شی کنار هم به n مکان نیاز است. برای قرار دادن اولین شی در خانه اول n حالت انتخاب داریم. برای قرار دادن دومین شی در خانه دوم n-1 حالت انتخاب داریم و به همین ترتیب برای قرار داردن n امین شی باقی مانده در خانه nام(خانه اخر) 1 حالت انتخاب داریم به این ترتیب بر طبق اصل ضرب برای قرار دادن این n شی در کنار هم در یک ردیف:
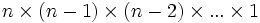
حالت وجود دارد که برابر می باشد با:
 به این ترتیب تعداد حالات جایگشت n شی دو به دو متمایز برابر
به این ترتیب تعداد حالات جایگشت n شی دو به دو متمایز برابر  است.
است.
مثال: به چندطریق می توان 5 کتاب متفاوت را کنار هم در یک قفسه قرار داد؟
پاسخ: برطبق توضیحات داده شده جواب برابر است با:
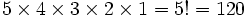
جایگشت خود می توان به 2 بخش تقسیم شود:
1- جایگشت با تکرار
2- جایگشت دوری
جایگشت با تکرار:
در قسمت قبل در مورد گونه ای جایگشت توضیح دادیم که در آن اشیا در به دو متمایز بودند اما گاهی ممکن است این اشیا در به دو متمایز نباشند و مثلا 3 عدد از انها از یک نوع باشند. چنین حالاتی را جایگشت باتکرار بررسی می کند.
با یک مثال روش محاسبه را توضیح می دهیم و سپس فرمولی برای محاسبه حالات بیان می کنیم:
فرض کنید می خواهیم فقط با ارقام 1.2.2.3 اعداد چهار رقمی بسازیم. یعنی عدد 1 یکبار، عدد 2 دو بار، عدد 3 یکبار
آمده باشد. بدیهی است که اگر این چهار رقم متمایز و به غیر صفر بودند تعداد اعداد برابر 24=!4 عدد می شد ولی اصل ضرب در این مورد ناخواسته دو عدد 2 را متمایز در نظر گرفته است و مثلا 1
223 و 1
223 را دو حالت متمایز در یظر گرفته است در حالی که این دو تفاوتی با هم ندارند. با نوشتن تعداد حالات متوجه میشویم که تعداد حالات واقعی این جایگشت !2 برابر مقدار محاسبه شده با اصل ضرب است به این ترتیب تعداد حالات واقعی برابر

است.
پس به این ترتیب تعداد k شی از یک نوع، به اندازه !K حالات اضافه تولید می کنند که باید از کل حالات که با اصل ضرب محاسبه می شود برداشته شوند.
تعریف: اگر n شی در اختیار داشته باشیم که
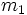
تا از نوع اول،
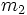
تا از نوع دوم،

تا از نوع سوم،....و

تا از نوع k ام باشند به گونه ای که
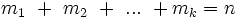
این n شی به

طریق می توانند در کنار هم قرار بگیرند.
در فرمول فوق علت تــقسیمها حذف حالات اضافی بوجود آمده است.
مثال: 8 پرچم موجوداند که 3تا به رنگ آبی و 2تا به رنگ قرمز و 3تا به رنگ سفید یکسان هستند.اگر قرار باشد این پرچم ها در یک ردیف کنار هم قرار گیرند چند علامت متمایز 8 پرچمی می توان ساخت؟
پاسخ:بر طبق مطالب فوق و فرمول ارائه شده تعداد حالات برابر است با:
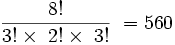
واضح است که در این سوال پرچمهای آبی !3 و قرمز !2 و سفید !3 حالت اضافی تولید می کنند که باید از حالات کل یعنی !8 حذف شوند.
جایگشت دوری:
تا به حال در مورد جایگشتهایی بحث کردیم که در مورد کنار هم قرار دادن چند شی در یک ردیف بودند. حال می خواهیم
گونه ای جایگشت را بررسی کنیم که در آن اشیا به صورت دوری در کنار هم قرار گیرند. با یک مثال نحوه محاسبه تعداد حالات جایگشت را توضیح می دهیم و در نهایت فرمولی برای محاسبه ان ارائه می دهیم:
فرض کنید می خواهیم تعداد حالاتی را که ممکن است 3 نفربه دور یک میز گرد بنشینند محاسبه کنیم. اگر قرار بر این بود که این افراد در یک ردیف کنار هم باشند این عمل به 6=!3 حالت صورت می پذیرفت. اما در نشستن به دور میز گرد مسئله متفاوت است چرا که بر طبق شکل در این جایگشت هر 3 حالت:
یک حالت محسوب می شوند چرا که هر یک دوران یافته دیگری در یک زاویه معین است و نیز هر سه حالت:
نیز یک حالت محسوب محسوب می شوند. پس تعداد کل حالات متمایز برابر دو عدد است.
به عبارت دیگر می توان A را یکجا قرار داده و B و C را در اطراف او نشاند. این کار به !2=!(2-3) طریق رخ می دهد.
نتیجه: در حالت کلی برای محاسبه جایگشت های دوری n شی دو به دو متمایز ابتدا یکی آنها را ملاک قرار داذه(فرق نمی کند کدام را) و سپس n-1 شی باقی مانده را به !(n-1) حالت به دور او قرار می دهیم.
پس تعداد حالات جایگشت دوری n شی دو به دو متمایز برابر است با:
