بسیاری از
عددهای اول به صورت جفتهایی به شکل p و p+2 هستند، مانند 3و5 ، 11و13 ، 29و31 . گمان میرود تعداد این گونه جفتها
نامتناهی باشد ولی تا کنون هیچ گام قطعی در راه اثبات این موضوع برداشته نشده است.
برون در 1919 اثبات کرد که بینهایت عدد p موجود است به طوری که هم p و هم p+2 حاصلضرب حداکثر 9 عدد اولند. این اثبات توسط سایر ریاضیدانان پیشرفت کرد به طوری که در 1924 ، رادماخر عدد برون را از 9 به 7 کاهش داد. در 1930 بوخشتاب این تعداد را به 6 و در 1938 به 5 رساند. ونگ با مفروض دانستن صورت تعمیم یافتهی
فرضیه ریمان در 1962 نشان داد که بینهایت عدد اول p موجود است به قسمی که p+2 حاصلضرب حداکثر 3 عدد اول است. با این حال بوخشتاب در 1965 و بدون در نظر گرفتن صحت فرضیه ریمان توانست اثبات کند که به ازای عدد c ثابتی ، بینهایت عدد اول p موجود است به قسمی که p+2 حاصلضرب حداکثر c عدد اول است.چن در مقالهای که در 1973 منتشر گردید اثبات کرد که عدد c=2 برای اثبات بوخشتاب کفایت میکند.
سی و پنج جفت ابتدایی اعداد اول دوقلو:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
قضیه
m و m+2 اعداد اول دوقلو هستند اگر و تنها اگر :
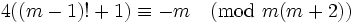
همچنین بببنید:
پیوندهای خارجی
اعداد اول دوقلو
اعداد اول دوقلو و ثابت برون
en.wikipedia.org
منابع
- ریاضیات چیست؟/ ریچارد کورانت ، هربرت رابینز ؛ ترجمه سیامک کاظمی _ تهران : نشر نی ، 1379.
- en.wikipedia.org